データドリフトをKLダイバージェンスで検証

- イントロダクション
- データドリフトとは
- KLダイバージェンスの基礎
3-1. KLダイバージェンスの定義と数式
3-2. KLダイバージェンスの特性
3-3. 定義論文の紹介 - データドリフトの検知にKLダイバージェンスを用いる
4-1. なぜKLダイバージェンスが有効か
4-2. G空間情報センターの人流データを用いた具体例
4-3. コロナ前後の人流データの比較 - 結果の解釈と考察
5-1. KLダイバージェンスの計算結果
5-2. データドリフトを検知する際の閾値設定 - まとめ
1. イントロダクション
機械学習モデルの精度を維持するためには、モデルが学習したデータの分布と、新しく入力されるデータの分布が一貫していることが重要です。しかし、現実世界では、データの分布が時間とともに変化することが避けられません。このデータの分布の変化は「データドリフト」と呼ばれ、データドリフトが生じると、モデルの予測精度が低下し、結果としてビジネス上の意思決定にも悪影響を及ぼす可能性があります。
本記事では、データドリフトを定量的に評価する手法の一つである「KLダイバージェンス(Kullback-Leibler Divergence)」を用いて、データドリフトを検知する方法を詳しく解説します。また、G空間情報センターが提供する人流データを用いて、コロナ前後のデータの分布変化を実際に計測し、データドリフトが発生していることを示します。
2. データドリフトとは
データドリフトとは、モデルが訓練された時点でのデータの分布と、運用中に入力されるデータの分布が異なる現象を指します。具体的には、訓練データと運用データの間で統計的な特徴(平均値や分散など)が異なることが原因となり、モデルの予測精度が劣化することがあります。
例えば、ECサイトにおける顧客の購買パターンが季節によって変わることや、外部要因(例: 新型コロナウイルスの影響)によって行動が大きく変化することなどが、データドリフトの一例です。
3. KLダイバージェンスの基礎
3-1. KLダイバージェンスの定義と数式
KLダイバージェンスは、情報理論の分野で提案された概念であり、二つの確率分布の間の「情報の損失」を測定する指標です。具体的には、ある確率分布\(P(x)\) から、別の確率分布\(Q(x)\) への変換に伴う「追加の情報」を表します。
KLダイバージェンスは次の数式で定義されます:\[D_{KL}(P || Q) = \sum_{x} P(x) \log\left(\frac{P(x)}{Q(x)}\right)\]
ここで、 \(P(x)\) は真の分布、 \(Q(x)\) は近似分布を示します。KLダイバージェンスは非対称であり、通常は非負の値を取ります。 \(D_{KL}(P∣∣Q)=0\) の場合、二つの分布は同一であることを意味します。
3-2. KLダイバージェンスの特性
KLダイバージェンスには以下の特性があります:
- 非対称性: \(D_{KL}(P || Q) \neq D_{KL}(Q || P)\)
- 非負性: KLダイバージェンスは常に0以上の値を取ります。
- 同一分布でのゼロ: 分布 \(P\) と \(Q\) が等しい場合、KLダイバージェンスはゼロになります。
これらの特性により、KLダイバージェンスはモデルの学習データと新しいデータ間の分布の違いを測定するための有用なツールとなります。
3-3. 定義論文の紹介
KLダイバージェンスは、Solomon KullbackとRichard Leiblerによって導入され、1951年の論文「On Information and Sufficiency」で詳しく説明されています。この論文で、KLダイバージェンスが初めて提案され、情報理論の重要な概念として確立されました。興味のある方はご一読ください。
Kullback, S., & Leibler, R. A. (1951). On Information and Sufficiency. The Annals of Mathematical Statistics, 22(1), 79-86.
4. データドリフトの検知にKLダイバージェンスを用いる
4-1. なぜKLダイバージェンスが有効か
データドリフトを検知するためには、訓練データと新しいデータ間での分布の違いを定量化する必要があります。KLダイバージェンスは、二つの分布の間の「情報の損失」を測定するため、データドリフトを捉えるのに適しています。
具体的には、訓練データから得られた確率分布 \(P(x)\) と、新しく得られたデータの分布 \(Q(x)\) を用いてKLダイバージェンスを計算し、その値が閾値を超える場合、データドリフトが発生していると判断できます。
4-2. G空間情報センターの人流データを用いた具体例
G空間情報センターが提供する人流データは、特定の地域における人々の移動パターンを示すデータです。このデータは、コロナ前後で大きな変化があり、データドリフトを検知する良い例となります。
本例では、コロナ前の人流データとコロナ後の人流データを比較し、その分布の変化をKLダイバージェンスを用いて定量化します。
簡単に、人流データの紹介を行います。今回は東京都のデータ(monthly_mdp_mesh1km_13(東京都))を分析に用いています。
| mesh1kmid | prefcode | citycode | year | month | dayflag | timezone | population |
| 53394519 | 13 | 13101 | 2019 | 2 | 0 | 0 | 16280 |
| 53394519 | 13 | 13101 | 2019 | 2 | 0 | 1 | 6496 |
| 53394519 | 13 | 13101 | 2019 | 2 | 0 | 2 | 10575 |
| 53394519 | 13 | 13101 | 2019 | 2 | 1 | 0 | 72551 |
| 53394519 | 13 | 13101 | 2019 | 2 | 1 | 1 | 10275 |
具体的には出典のマスタファイルをご一読頂きたいと思いますが、上表のサンプルデータのmesh1kmid=53394519は、「緯度35.6791649, 経度139.743744」を中心とする1kmメッシュの人流データを表していることになります。
また、人流データは、各メッシュごとに、
- dayflag⇒0:休日、1:平日、2:全日
- timezone⇒0:昼、1:深夜、2:終日
の3×3=9通りのデータが1つのデータベースとして整備されています。今回は、簡単のため、dayflag=2(全日)、timezone=2(終日)のデータを分析に用いることにします。
出典:「全国の人流オープンデータ」(国土交通省)
4-3. データ前処理
まず、コロナ前の人流データとコロナ後の人流データを取得し、各地点での人流の分布を計算します。その後、KLダイバージェンスを計算し、分布間の変化を数値的に評価します。
各メッシュ地点ごとの人口を1レコードとし、それらを月単位で集計することで分布を作成し、KLダイバージェンスの計算に使用しています。
以下に、前処理コードを掲載します。今回はGoogle Driveに人流データを格納し、Google Colaboratory上で分析を実施しました。適宜、ファイルパスを変えて実行してください。
import os
import zipfile
os.chdir("/content/drive/MyDrive/monthly_mdp_mesh1km_13/13")
import glob
import pandas as pd
from tqdm import tqdm
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import numpy as np
!pip install japanize_matplotlib
import japanize_matplotlib
from datetime import datetime
# 空のデータフレームを定義
df = pd.DataFrame()
# 全ての年月データを取り込む
for zip in tqdm( glob.glob("./*/*/*") ):
with zipfile.ZipFile(zip, 'r') as zip_ref:
zip_ref.extractall('/content/extracted_files')
temp_df = pd.read_csv('/content/extracted_files/monthly_mdp_mesh1km.csv')
df = pd.concat([df, temp_df])
# 昼夜平均、かつ全日でフィルタ
df_22 = df.query("timezone == 2 & dayflag == 2").copy()
# 2019, 2020, 2021年すべての年月で欠損がない地域を抽出
mesh1kmid_list = df_22.groupby("mesh1kmid")["citycode"].count().reset_index().query("citycode == 36")["mesh1kmid"].tolist()
# 2019, 2020, 2021年すべての年月で欠損がない地域でフィルタを実施
df_22_filetered = df_22.query("mesh1kmid in {}".format(mesh1kmid_list)).copy()
# yyyymm形式のカラムを作成
df_22_filetered["yyyymm"] = df_22_filetered.apply(lambda row:"{:04d}{:02d}".format(row["year"], row["month"]), axis=1).astype("int")5. 結果の解釈と考察
5-1. KLダイバージェンスの計算結果
以下のコードを用いることで、KLダイバージェンスを計算および可視化することが可能です。今回は、2019/01~2019/10までを学習期間とし、2019/11~でデータドリフトが起きていないか検証するためKLダイバージェンスを計算しました。また、KLダイバージェンスを計算するにあたって、ヒストグラムのbin数は今回50としています。
def kl_divergence(train_data, new_data, bin_count=50):
"""
Calculate the Kullback-Leibler divergence between two datasets.
Parameters:
train_data (array-like): The data used to train the model (e.g., 10,000 points).
new_data (array-like): The new dataset to compare against the training data (e.g., 1,000 points).
bin_count (int): The number of bins to use for the histogram.
Returns:
float: The KL divergence value.
"""
# Create histograms for both datasets
p_hist, bin_edges = np.histogram(train_data, bins=bin_count, density=True)
q_hist, _ = np.histogram(new_data, bins=bin_edges, density=True)
# Normalize the histograms to get probability distributions
p_hist /= np.sum(p_hist)
q_hist /= np.sum(q_hist)
# Avoid division by zero and log of zero by adding a small value (epsilon)
epsilon = 1e-10
p_hist = p_hist + epsilon
q_hist = q_hist + epsilon
# Calculate KL divergence
return np.sum(p_hist * np.log(p_hist / q_hist))
kld_list = []
# 201901-201910までを学習期間とし、以降1か月ごとにKL距離を計算する
for yyyymm in df_22_filetered[["yyyymm"]].sort_values("yyyymm")["yyyymm"].unique()[10:]:
kld = kl_divergence(
df_22_filetered.query("yyyymm <= 201910")["population"],
df_22_filetered.query("yyyymm == {}".format(yyyymm))["population"])
kld_list.append([yyyymm, kld])
# pd.dataframeにする
df_kld = pd.DataFrame(kld_list, columns=["yyyymm", "kld"])
# 描画用にdatetime形式に変換しておく
df_kld["yyyymm_datetime"] = df_kld["yyyymm"].apply(lambda x: datetime(int(str(x)[:4]), int(str(x)[4:]), 1))
# グラフを定義
plt.figure(figsize=(10, 5), tight_layout=True)
ax = plt.subplot()
# COVID-19前
ax.plot(
df_kld["yyyymm_datetime"][:5],
df_kld["kld"][:5],
color = "black",
label='Before the emergence of COVID-19'
)
# COVID-19後
ax.plot(
df_kld["yyyymm_datetime"][4:],
df_kld["kld"][4:],
color="red",
label='After the emergence of COVID-19'
)
# XY軸のラベルの文字サイズを設定
ax.tick_params(axis='x', labelsize=8)
ax.tick_params(axis='y', labelsize=8)
# XY軸のタイトルを設定
ax.set_ylabel("KL Divergence", fontsize=9)
ax.set_xlabel("Date (YYYY-MM)", fontsize=9)
# 判例を表示
legend = ax.legend(loc='upper right', frameon=True, shadow=True, title="[explanatory note]", facecolor="lightgrey")
# 全体のタイトルを設定
plt.suptitle("KL Divergence Between the Training Period Distribution(Up to 201910) and Monthly Distributions(From 201911)", fontsize=10)
# 画像を出力
plt.savefig("/content/extracted_files/kld.png", dpi=300)
# グラフを描画
plt.show()コロナ前後での人流データの分布をKLダイバージェンスで比較した結果、2020/04以降に大きなデータドリフトが発生していることが確認されました。これにより、緊急事態宣言を代表とする外的要因が人々の行動に影響を与え、データドリフトを引き起こしたことが明らかです。
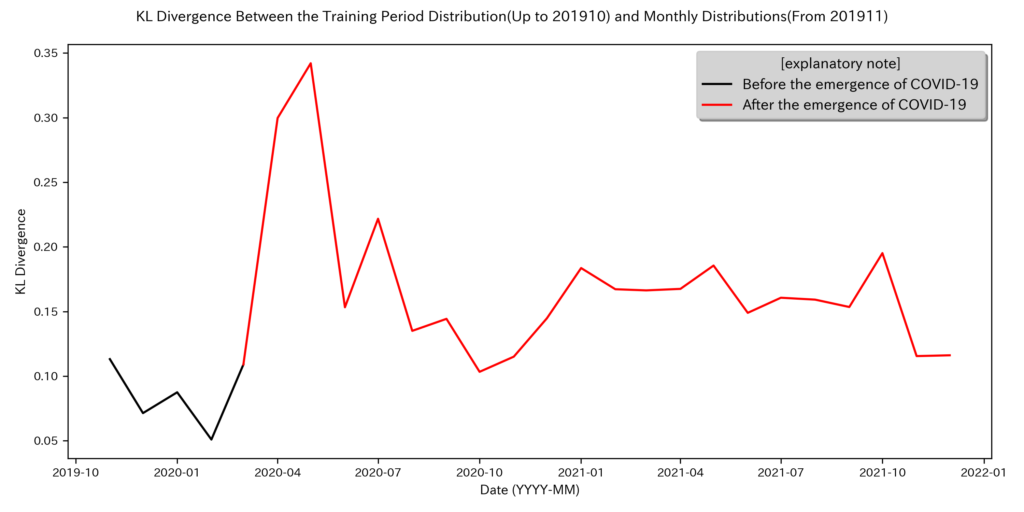
なお、上図を下表を比較することで、緊急事態の発令タイミングとKLダイバーシティの増加がおおよそ連動していることが見て取れます。
| 発令 | 発令開始日 | 解除日 | 期間 |
| 第1回 | 2020年4月7日 | 2020年5月25日 | 49日間 |
| 第2回 | 2021年1月8日 | 2021年3月21日 | 72日間 |
| 第3回 | 2021年4月25日 | 2021年6月20日 | 56日間 |
| 第4回 | 2021年7月12日 | 2021年9月30日 | 81日間 |
5-2. データドリフトを検知する際の閾値設定
なお、KLダイバージェンスにおいて、データドリフトが起きているかを判断する明確な「閾値」は存在しません。これは、KLダイバージェンスが数値的にどの程度の差異を示すかはデータセットの特性や分布によって異なるためです。
ただし、実際にデータドリフトを検出する際には、次のようなアプローチが取られることがあります。
- ベースラインの設定: 訓練データに基づいてKLダイバージェンスのベースラインを設定します。その後、新しいデータセットと比較した際に、ベースラインを大きく上回る場合にデータドリフトが発生していると判断する方法です。
- ヒューリスティックな判断: ドメインの知識や過去の経験に基づき、KLダイバージェンスの値が特定の基準を超えた場合にドリフトが起きていると判断することがあります。この基準はデータの分布やビジネス上の許容範囲に依存します。
- シミュレーションやテスト: シミュレーションを用いて、どの程度のKLダイバージェンスが実際にモデルの性能に影響を与えるかをテストする方法もあります。これにより、実務的に影響が出る範囲を基に閾値を設定することが可能です。
- 統計的検定: KLダイバージェンスと他の統計的検定を組み合わせて、ドリフトの有無を検証する方法もあります。例えば、二つのデータセットの平均や分散の差が有意かどうかを検定し、その結果をKLダイバージェンスの値と照らし合わせて判断します。
要するに、KLダイバージェンスに基づいてデータドリフトを判断する際には、明確な数値的な閾値はなく、データセットやモデルの特性に応じたベースラインや基準を設定する必要があります。ドリフトがモデルの性能にどの程度影響を与えるかを評価し、その結果をもとに判断することが重要です。
6. まとめ
本記事では、KLダイバージェンスを用いてデータドリフトを検知する方法について解説しました。特に、G空間情報センターが提供する人流データを用いた具体例を通して、コロナ前後の人流の変化を定量的に評価しました。
データドリフトの検知は、機械学習モデルの精度維持において非常に重要なプロセスです。KLダイバージェンスは、その特性から有効な指標となり得ます。今後も継続的なモニタリングと適切な対応を行うことで、モデルのパフォーマンスを維持し続けることが求められます。

同カテゴリーの記事はこちら







