SHAP, LIMEを用いた予測根拠の定量化

- イントロダクション
- ブラックボックスモデルの透明性の必要性
2-1. 機械学習におけるブラックボックス問題とは
2-2. 透明性の確保が求められる理由
2-3. モデルの解釈可能性を高める手法の概要 - LIMEとSHAPによる予測根拠の定量化
3-1. LIMEの理論と仕組み
3-2. SHAPの理論と仕組み - 実際のデータを用いた検証
4-1. カリフォルニアの住宅価格データセットを用いた回帰タスク
4-2. 乳がんデータセットを用いた分類タスク - まとめ
1. イントロダクション
機械学習の技術が進展する中で、モデルの性能向上と引き換えにその内部構造が複雑化し、一般的に「ブラックボックス」と称される状況が増えています。ブラックボックスモデルとは、入力に対して出力を生成する過程が理解しにくい、あるいは全く理解できないモデルを指します。このようなモデルは、高い予測精度を誇る一方で、その決定に対する説明責任を果たすことが困難であり、特に金融、医療、法務などの重要な分野での導入には慎重を要します。
そこで、機械学習モデルに透明性を与える手法として注目されているのが、LIME(Local Interpretable Model-agnostic Explanations)とSHAP(SHapley Additive exPlanations)です。本記事では、これらの手法を用いて、ブラックボックスな機械学習モデルにどのように透明性を与え、予測根拠を定量化するかについて検証していきます。
アルゴリズム設計における透明性については、以下の記事でも触れています。
2. ブラックボックスモデルの透明性の必要性
この章では、ブラックボックスモデルで、なぜ透明性が求められるかについて解説をしていきます。
2-1. 機械学習におけるブラックボックス問題とは
機械学習モデルは、多くのデータを学習し、そのデータの中に存在するパターンを捉えて予測を行います。例えば、ニューラルネットワークやブースティングなどのモデルは非常に高い予測性能を誇りますが、その内部の動作原理が複雑であるため、どの特徴量がどのように予測に影響を与えているのかを説明するのが難しいです。
2-2. 透明性の確保が求められる理由
ブラックボックスモデルの透明性を確保する理由は多岐にわたります。まず、透明性はモデルの結果に対する信頼性を向上させます。また、予測結果に対する根拠を明らかにすることで、モデルの意思決定プロセスを人間が理解しやすくなり、モデルの改善や異常検知が容易になります。さらに、特定の業界では法律や規制によってモデルの解釈可能性が求められることもあります。
2-3. モデルの解釈可能性を高める手法の概要
LIMEとSHAPは、ブラックボックスモデルの透明性を向上させる代表的な手法です。LIMEは、ローカルな領域で単純なモデルを作成し、そのモデルを用いて予測の説明を行います。一方、SHAPは、ゲーム理論に基づく手法であり、各特徴量の影響度を計算して予測結果に対する寄与を明らかにします。
3. LIMEとSHAPによる予測根拠の定量化
この章では、LIMEとSHAPの理論および数式、利点と限界をそれぞれ述べていきます。
3-1. LIMEの理論と仕組み
LIMEは、ある予測の周辺において、簡易で解釈可能なモデル(例えば線形モデル)を適用することで、その予測の根拠を説明する手法です。具体的には、LIMEは、まず元のデータセットからランダムにサンプルを生成し、それらに基づいて単純化されたモデルを構築します。次に、このモデルを用いて、どの特徴量が予測にどのように影響を与えているかを評価します。
LIMEをもっと深く学びたい方は、以下の論文をご参照ください。
Ribeiro, M. T., Singh, S., & Guestrin, C. (2016). “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 1135-1144). ACM.
3-1-1. LIMEの数式的説明
LIMEの数式的な枠組みは次のように表されます。ある予測モデル \(f\) に対して、LIMEはその予測値 \(f(x)\) の近似を目的とします。LIMEでは、局所領域 \(z\) における簡易モデル \(g\) を最適化することで、以下のようなコスト関数 \(\mathcal{L}\) を最小化します。
\[\mathcal{L}(f, g, \pi_x) = \sum_{z \in Z} \pi_x(z) \left( f(z) – g(z) \right)^2 + \Omega(g)\]
ここで、\(\pi_x(z)\) は局所的な重要度を表し、\(\Omega(g)\) はモデルの複雑さに対するペナルティです。
3-1-2. LIMEの利点と限界
LIMEの利点は、モデルに依存しない(Model-agnostic)点にあります。すなわち、どのような予測モデルに対しても適用可能であることです。しかし、局所領域に限定されているため、グローバルな解釈は困難であり、また、近似モデルが必ずしも正確でない場合があります。
3-2. SHAPの理論と仕組み
SHAPは、ゲーム理論のシャープレイ値(Shapley Value)を利用して、各特徴量が予測結果にどのように寄与しているかを計算する手法です。シャープレイ値は、協力ゲームにおける各プレイヤーの貢献度を公平に分配する方法であり、これを機械学習の文脈に適用することで、各特徴量の影響度を定量化します。
SHAPをもっと深く学びたい方は、以下の論文をご参照ください。
Lundberg, S. M., & Lee, S. I. (2017). A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (pp. 4765-4774). NIPS.
3-2-1. SHAPの数式的説明
SHAPの枠組みでは、予測値 \(f(x)\) は、各特徴量の寄与の和として表されます。
\[f(x) = \phi_0 + \sum_{i=1}^{M} \phi_i\]
ここで、\(\phi_i\)は特徴量\(i\)のシャープレイ値を表し、\(\phi_0\)はベースライン値です。シャープレイ値 \(\phi_i\)は以下の式で計算されます。
\[\phi_i = \sum_{S \subseteq N \setminus {i}} \frac{|S|!(|N|-|S|-1)!}{|N|!} \left( f(S \cup {i}) – f(S) \right)\]
ここで、\(S\)は特徴量の部分集合、\(N\)は全特徴量の集合です。
3-2-2. SHAPの利点と限界
SHAPの利点は、各特徴量の影響度を公平かつ一貫した方法で計算できる点にあります。また、LIMEとは異なり、グローバルな解釈も可能です。しかし、計算コストが高いため、大規模なデータセットや複雑なモデルに対しては適用が難しい場合があります。
4. 実際のデータを用いた検証
以下では、実際にSHAPおよびLIMEを使って、予測根拠の定量化を実施してみたいと思います。
以下は、分析に必要なライブラリです。
# その他ライブラリ
import matplotlib.pyplot as plt
# モデル学習ライブラリ
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing, load_breast_cancer
from xgboost import XGBRegressor, XGBClassifier
# LIMEライブラリ
!pip install lime
import lime
import lime.lime_tabular
import webbrowser
# SHAPライブラリ
!pip install shap
import shap4-1. カリフォルニアの住宅価格データセットを用いた回帰タスク
まず、カリフォルニアの住宅価格データセットを用いて、回帰タスクに対するLIMEとSHAPの適用例を見てみます。このデータセットには、住宅の平均部屋数や経済状態などの特徴量が含まれており、これらを用いて住宅価格を予測します。xgboostを用いて予測を行い、その後LIMEとSHAPで各特徴量の寄与を可視化します。
今回は、全体のデータの80%を学習データとし、残り20%を評価データとします。評価データのindex=0(回帰予測で予測した住宅価格::4.2954483)について、LIMEおよびSHAPで可視化を試みてみようと思います。また、LIMEにおいては何個の変数を用いて可視化するかを選べるため、今回は=5で実行します。
# 回帰タスク
x_regressor = fetch_california_housing()["data"]
y_regressor = fetch_california_housing()["target"]
feature_name = fetch_california_housing()["feature_names"]
# 訓練データとテストデータに分割
X_train_regressor, X_test_regressor, y_train_regressor, y_test_regressor =train_test_split(
x_regressor, y_regressor, test_size=0.2, random_state=1)
# モデルの学習
model_regressor = XGBRegressor()
model_regressor.fit(X_train_regressor, y_train_regressor)
i = 0 # 任意のインデックス
print("予測値:", model_regressor.predict(X_test_regressor[[i]])[0])
# LIMEの解釈器を初期化
explainer = lime.lime_tabular.LimeTabularExplainer(X_train_regressor, feature_names=feature_name, mode='regression')
# 1つのデータポイントに対する解釈を行う
exp = explainer.explain_instance(X_test_regressor[i], model_regressor.predict, num_features=5)
# 結果をHTMLファイルとして保存
exp.save_to_file('lime_explanation_regressor.html')
# SHAP値を計算
explainer = shap.TreeExplainer(model_regressor)
shap_values = explainer.shap_values(X_test_regressor)
i = 0 # 任意のインデックスを指定
force_plot = shap.force_plot(explainer.expected_value, shap_values[i], X_test_regressor[i], feature_names=feature_name)
# フォースプロットをHTMLとして保存
shap.save_html('shap_force_plot_regressor.html', force_plot)
# ウォーターフォールプロットを生成して保存
shap.waterfall_plot(shap.Explanation(values=shap_values[i],
base_values=explainer.expected_value,
data=X_test_regressor[i],
feature_names=feature_name))
# プロットを画像として保存 (PNG形式)
plt.savefig('shap_waterfall_plot_regressor.png')
plt.show()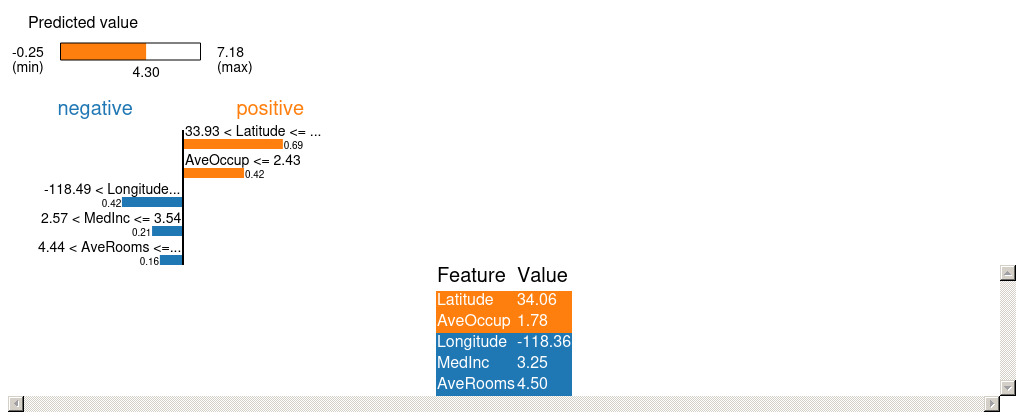
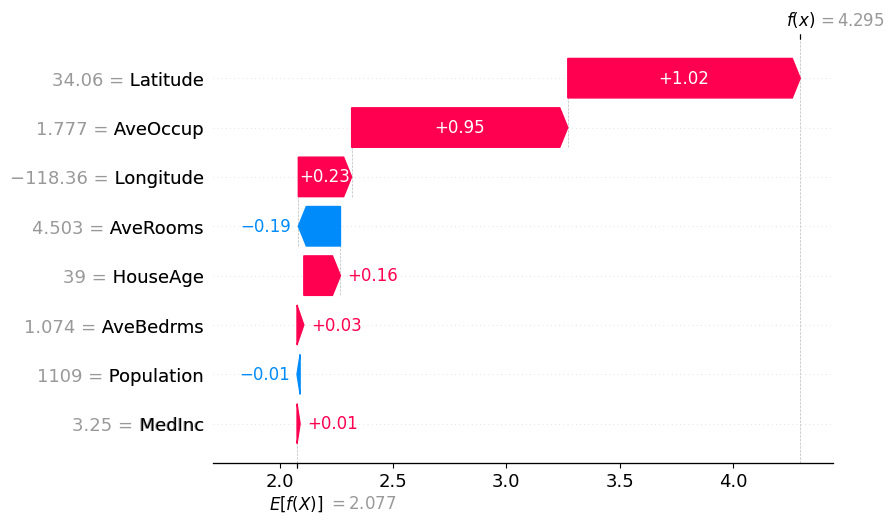
上記の可視化結果より、LatitueおよびAveOccupが正方向に強く寄与していることがわかります。
4-2. 乳がんデータセットを用いた分類タスク
次に、乳がんデータセットを用いた分類タスクでの検証を行います。このデータセットは、乳がんが良性か悪性かを予測するためのものであり、特徴量として腫瘍の大きさや形状などが含まれます。xgboostを用いて分類モデルを構築し、LIMEとSHAPを用いて特徴量の重要度を分析します。
住宅価格の回帰モデルと同様に、全体のデータの80%を学習データとし、残り20%を評価データとします。評価データのindex=0(分類で悪性と予測する確率値:0.889238)について、LIMEおよびSHAPで可視化を試みてみます。また、LIMEにおいては何個の変数を用いて可視化するかを選べるため、今回は=5で実行します。
# 分類タスク
x_classifier = load_breast_cancer()["data"]
y_classifier = load_breast_cancer()["target"]
feature_name = load_breast_cancer()["feature_names"]
# 訓練データとテストデータに分割
X_train_classifier, X_test_classifier, y_train_classifier, y_test_classifier =train_test_split(
x_classifier, y_classifier, test_size=0.2, random_state=1)
# モデルの学習
model_classifier = XGBClassifier()
model_classifier.fit(X_train_classifier, y_train_classifier)
i = 0 # 任意のインデックス
print("予測値:", model_classifier.predict_proba(X_test_classifier[[i]])[0])
# LIMEの解釈器を初期化
explainer = lime.lime_tabular.LimeTabularExplainer(
X_train_classifier, feature_names=feature_name, mode='classification')
# 1つのデータポイントに対する解釈を行う
exp = explainer.explain_instance(X_test_classifier[i], model_classifier.predict_proba, num_features=5)
# 結果をHTMLファイルとして保存
exp.save_to_file('lime_explanation_classification.html')
# SHAP値を計算
explainer = shap.TreeExplainer(model_classifier)
shap_values = explainer.shap_values(X_test_classifier)
i = 0 # 任意のインデックスを指定
force_plot = shap.force_plot(
explainer.expected_value,
shap_values[i],
X_test_classifier[i],
feature_names=feature_name)
# フォースプロットをHTMLとして保存
shap.save_html('shap_force_plot_classification.html', force_plot)
# ウォーターフォールプロットを生成して保存
shap.waterfall_plot(shap.Explanation(values=shap_values[i],
base_values=explainer.expected_value,
data=X_test_classifier[i],
feature_names=feature_name))
# プロットを画像として保存 (PNG形式)
plt.savefig('shap_waterfall_plot_classification.png')
plt.show()
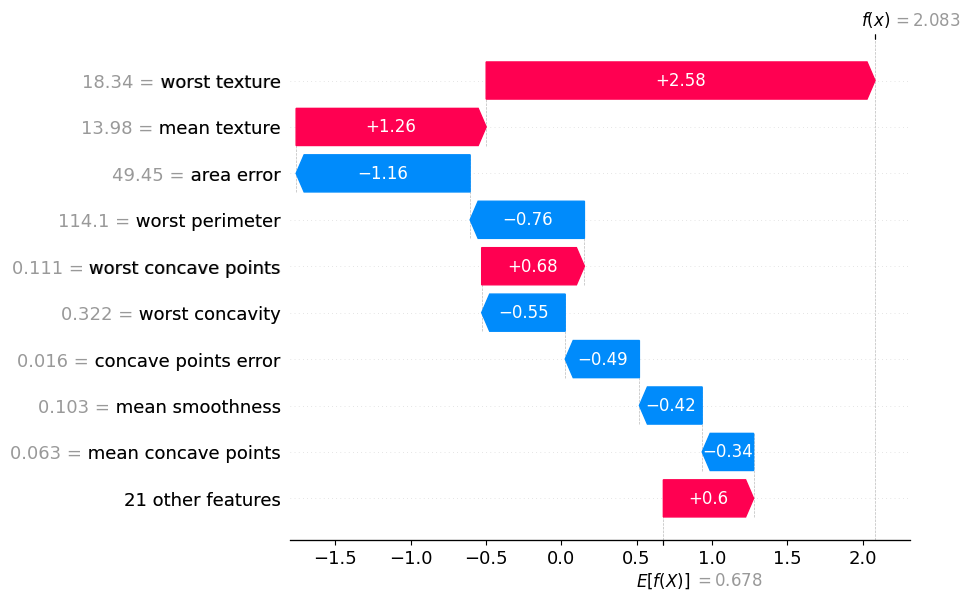
上記の可視化結果より、worst textureが正方向に強く寄与していることがわかります。
注意点として、SHAPはシグモイド変換前の値が表示されているため、\(\frac{1}{1+\epsilon^{-2.083}}=0.89\)という計算を行う必要があります。
5. まとめ
本記事では、LIMEとSHAPという2つの代表的な手法を用いて、ブラックボックスな機械学習モデルに透明性を与える試みを紹介しました。LIMEは局所的な解釈が可能であり、SHAPはグローバルな解釈を提供します。それぞれの手法には利点と限界があり、用途に応じて適切な手法を選択することが重要です。機械学習の分野における透明性の確保は、今後ますます重要になると考えられます。この記事が、皆様のモデル開発において有益な参考となれば幸いです。





